Ley de mortalidad de Gompertz-Makeham

La ley de Gompertz-Makeham establece que la tasa de mortalidad humana es la suma de un componente dependiente de la edad (la función de Gompertz, llamada así por Benjamin Gompertz),^[1]​ que aumenta exponencialmente con la edad^[2]​ y un componente independiente de la edad (el Término de Makeham, llamado así por William Makeham).^[3]​ En un entorno protegido donde las causas externas de muerte son raras (condiciones de laboratorio, países de baja mortalidad, etc.), el componente de mortalidad independiente de la edad es a menudo insignificante. En este caso, la fórmula se simplifica a una ley de mortalidad de Gompertz. En 1825, Benjamin Gompertz propuso un aumento exponencial de las tasas de mortalidad con la edad.

La ley de mortalidad de Gompertz-Makeham describe la relación de la edad con la mortalidad humana con bastante precisión en la ventana de edad de aproximadamente 30 a 80 años. En edades más avanzadas, algunos estudios han encontrado que las tasas de mortalidad aumentan más lentamente, un fenómeno conocido como desaceleración de la mortalidad en la vejez,^[2]​ aunque estudios más recientes no están de acuerdo.^[4]​

La disminución de la tasa de mortalidad humana antes de la década de 1950 se debió principalmente a una disminución en el componente de mortalidad independiente de la edad (Makeham), mientras que el componente de mortalidad dependiente de la edad (Gompertz) se mantuvo sorprendentemente estable.^[2]​^[5]​ Desde la década de 1950, ha comenzado una nueva tendencia de mortalidad en forma de una disminución inesperada de las tasas de mortalidad en edades avanzadas y una "rectangularización" de la curva de supervivencia.^[6]​^[7]​

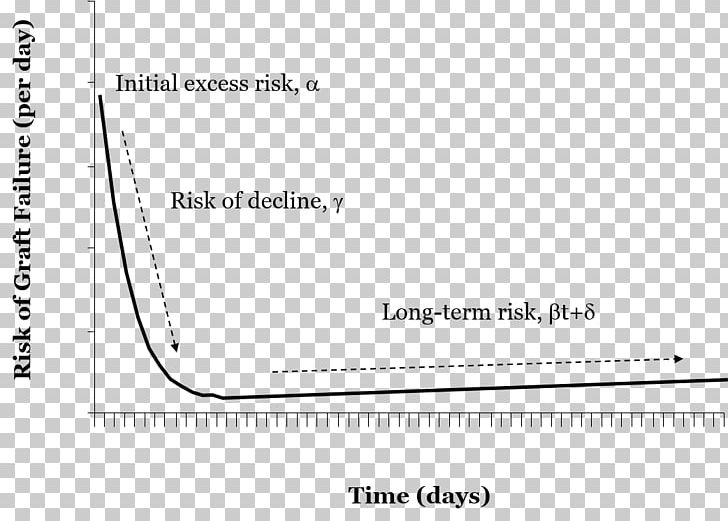
La función de riesgo para la distribución de Gompertz-Makeham se caracteriza con mayor frecuencia como ${\displaystyle h(x)=\alpha e^{\beta x} \lambda }$. La magnitud empírica del parámetro beta es de aproximadamente .085, lo que implica una duplicación de la mortalidad cada .69 / .085 = 8 años (Dinamarca, 2006).

La función cuantil se puede expresar en una expresión de forma cerrada utilizando la función W de Lambert:^[8]​

${\displaystyle Q(u)={\frac {\alpha }{\beta \lambda }}-{\frac {1}{\lambda }}\ln(1-u)-{\frac {1}{\beta }}W_{0}\left[{\frac {\alpha e^{\alpha /\lambda }(1-u)^{-(\beta /\lambda )}}{\lambda }}\right]}$

La ley de Gompertz es la misma que una distribución de Fisher-Tippett para el negativo de la edad, restringida a valores negativos para la variable aleatoria (valores positivos para la edad).

Véase también

• Biodemografía
• Biodemografía de la longevidad humana
• Gerontología
• Demografía
• Tabla de vida
• Vida útil máxima
• Teoría de la confiabilidad del envejecimiento y la longevidad.

Referencias